Rekurzivní funkce je pojmenování pro funkce, které volají samy sebe. Je dobré o nich vědět, protože můžou někdy výrazně zjednodušit řešení problému.

Ukázka rekurzivní funkce je

void rekurze() {
    rekurze();
}

Kdybychom takovou funkci zavolali, tak se nedočkáme úspěšného konce. Můžeme si to demonstrovat na následujícím programu

#include <stdio.h>

void rekurze() {
    rekurze();
}

int main()
{
    rekurze();

    return 0;
}

Takový program poběží teoreticky nekonečně dlouho. Ve skutečnosti ale programu dojde paměť v počítači a program se ukončí s chybou stack overflow. Proto je důležité u každé rekurzivní funkce mít podmínkou, kdy program skončí (ukončující podmínku).

Příkladem rekurzivní funkce může být výpočet faktoriálu. Pro zopakování faktoriálu např. zde.

Pro faktoriál platí

  1. pokud n = 0, pak faktoriál se rovná 1
  2. jinak platí, že n faktoriál se rovná n krát n - 1 faktoriál (n! = n*(n-1)!)

Pokud se výpočet faktoriálu pokusíme naprogramovat, tak si nejdříve můžeme udělat ukončující podmínku

#include <stdio.h>

int faktorial(int n) {
    if (n == 0) {
        return 1;
    }

    return ...;
}

int main()
{
    int vysledek = faktorial(5);

    return 0;
}

To je náše podmínka, která nám zastaví nekonečnou rekurzi. V každé rekurzivní funkci musí být nějaká podmínka, která výpočet zastaví a již znova nezavolá danou funkci.

Nyní můžeme naprogramovat druhou část funkce. Pokud n není 0, tak se má vrátít n * (n - 1)!.

To můžeme naprogramovat následovně

#include <stdio.h>

int faktorial(int n) {
    if (n == 0) {
        return 1;
    }

    return n * faktorial(n - 1);
}

int main()
{
    int vysledek = faktorial(5);
    printf("Vysledek %i\n", vysledek);

    return 0;
}

Jak výpočet probíhá?

Volání Návratová hodnota Výsledek
faktorial(5) return 5 * faktorial(4) 120 (5 * 24)
faktorial(4) return 4 * faktorial(3) 24 (4 * 6)
faktorial(3) return 3 * faktorial(2) 6 (3 * 2)
faktorial(2) return 2 * faktorial(1) 2 (2 * 1)
faktorial(1) return 1 * faktorial(0) 1 (1 * 1)
faktorial(0) return 1 1

Pokud si to odkrokujeme, tak dostáváme

  1. Zavolá se funkce faktorial(5)
  2. Zkontroluje se podmínka - je 5 rovno 0? Ne, IF se nevyhodnotí
  3. zavolá se 5 * faktorial(4)
  4. Zkontroluje se podmínka - je 4 rovno 0? Ne, IF se nevyhodnotí
  5. zavolá se 4 * faktorial(3)
  6. Zkontroluje se podmínka - je 3 rovno 0? Ne, IF se nevyhodnotí
  7. zavolá se 3 * faktorial(2)
  8. Zkontroluje se podmínka - je 2 rovno 0? Ne, IF se nevyhodnotí
  9. zavolá se 2 * faktorial(1)
  10. Zkontroluje se podmínka - je 1 rovno 0? Ne, IF se nevyhodnotí
  11. zavolá se 1 * faktorial(0)
  12. Zkontroluje se podmínka - je 0 rovno 0? Ano, IF se vyhodnotí
  13. Vrátí se hodnota 1 jako výsledek faktorial(0)
  14. 1 * faktorial(0) se nahradí za 1 * 1
  15. Vrátí se hodnota 1 jako výsledek faktorial(1)
  16. 2 * faktorial(1) se nahradí za 2 * 1
  17. Vrátí se hodnota 2 jako výsledek faktorial(2)
  18. 3 * faktorial(2) se nahradí za 3 * 2
  19. Vrátí se hodnota 6 jako výsledek faktorial(3)
  20. 4 * faktorial(3) se nahradí za 4 * 6
  21. Vrátí se hodnota 24 jako výsledek faktorial(4)
  22. 5 * faktorial(4) se nahradí za 5 * 24
  23. Vrátí se hodnota 120 jako výsledek faktorial(5)
  24. Hodnota 120 se uloží do proměnné vysledek ve funkci main
  25. Hodnota vysledek se vytiskne
  26. Program se ukončí pomocí return 0

Obecný výpočet rekurzivní funkce probíhá vždy tak, že se nejdříve výpočet zanořuje směrem dolů (volá se rekurzivní funkce dále a dále). Výpočet se zanořuje tak dlouho, než narazí na ukončovací podmínku (v našem případě pro faktoriál n == 0). Jakmile se narazí na ukončovací podmínku, tak se výpočet začne zase vynořovat (volání rekurzivní funkce se nahrazují za hodnoty).

Na diagramu by to vypadalo následovně

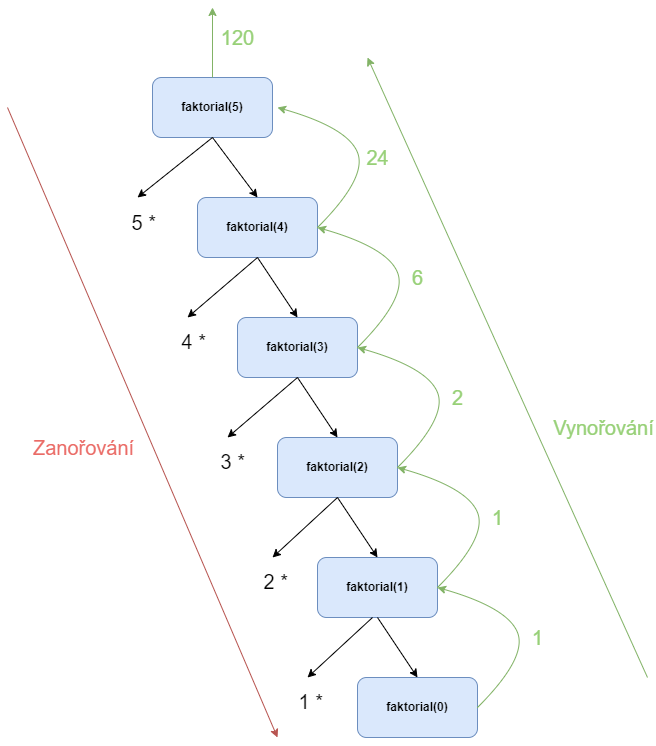
faktorial

Vztah rekurze a iterace

Obecně se programy s rekurzí dají přepsat na programy bez rekurze se zachováním funkčnosti. Náš program na výpočet faktoriálu by šlo napsat bez použití rekurze následovně

#include <stdio.h>

int faktorial(int n) {
    int vysledek = 1;

    while (n > 1) {
        vysledek = vysledek * n;
        n = n - 1;
    }

    return vysledek;
}

int main()
{
    int vysledek = faktorial(5);
    printf("Vysledek %i\n", vysledek);

    return 0;
}

Některé programy je však mnohem jednodušší napsat pomocí rekurze a bylo by mnohem náročnější je napsat bez rekurze.

Je nutné si dát pozor, že použití rekurze může mít negativní vliv na výkon programu. Velké rekurze si berou hodně zdrojů počítače a pro velké množství zanoření nemusí takový program ani nikdy doběhnout.

Odkazy

Následující kapitola: Čistý kód

GitHub diskuze k této kapitole

Zpátky na přehled

Předchozí kapitola: Struktura Switch